What is Modular Arithmetic?
Where \(A\) and \(B\) are integers, we can write:
$$ \frac{A}{B} = Q \text{ remainder } R $$
Using the same \(A, B, Q, \text{ and } R\) as above, we have:
$$ A \text{ mod } B = R $$
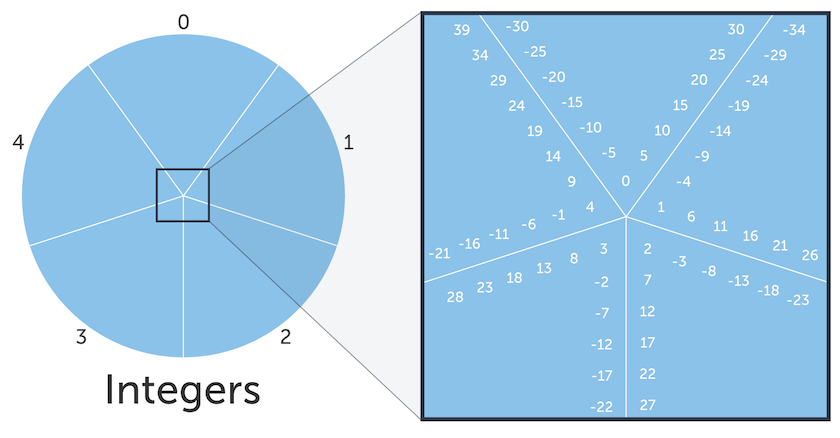
\(A \text{ mod } B\) can be visualized as taking \(A\) steps on a clock that runs from \(0\) to \(B-1\). If the number is positive we step clockwise, if it’s negative we step counterclockwise.
Examples: \(23 \text{ mod } 6 = 5; -17 \text{ mod } 7 = 4 \)
If we have \(A \text{ mod } B\) and we increase \(A\) by a multiple of \(B\), we will end up in the same spot, i.e.
$$ A \text{ mod } B = (A + K \cdot B) \text{ mod } B \text{ for any integer } K $$
Congruence Modulo
\(11 \text{ mod } 5 = 1\), and \(16 \text{ mod } 5 = 1\). Therefore, \(11\) and \(16\) are in the equivalence class for \(1\). This is expressed mathematically as \(16 \equiv 11 \text{ mod } 5)\), and read as, “16 is congruent to 11 modulo 5”.
More generally:
$$ A \equiv B \ (\text{mod } C) $$
Note that the \((\text{mod } C)\) is applied to both \(A\) and \(B\). This is different from \(A \text{ mod } C\): \(16 \ne 11 \text{ mod } 5\).
Notice that in the same equivalence class, the difference between any two values is some multiple of \(C\), e.g. in the equivalence class for \(1\), we have: \(…, 1 - 3C, 1 - 2C, 1 - C, 1 + C, 1 + 2C, 1 + 3C, …\)
Therefore, the following statements are equivalent:
$$ A \equiv B \ (\text{mod } C) $$ $$ A \text{ mod } C = B \text{ mod } C $$ $$ C | (A - B) \text{ (The | symbol means divides, or is a factor of)} $$ $$ A = B + K \cdot C \text{ (where } K \text{ is some integer)} $$
Congruence Modulo is an Equivalence Relation
An equivalence relation defines how we can partition our set of values into equivalence classes. The congruence modulo \(C\) is an equivalence relation that partitions the integers into \(C\) different equivalent classes, where in each equivalence class, all contained values are congruent modulo \(C\).
Equivalence relations have the following properties:
- They are reflexive: \(A\) is related to \(A\).
- They are symmetric: if \(A\) is related to \(B\), then \(B\) is related to \(A\).
- They are transitive: if \(A\) is related to \(B\), and \(B\) is related to \(C\), then \(A\) is related to \(C\).
Specifically, for the congruence modulo \(C\) equivalence relation:
- \(A \equiv A \ (\text{mod }C) \)
- If \(A \equiv B \ (\text{mod }C)\), then \(B \equiv A \ (\text{mod }C)\)
- If \(A \equiv B \ (\text{mod }C)\), and \(B \equiv D \ (\text{mod }C)\), then \(A \equiv D \ (\text{mod }C)\)
Programmer’s Note
The result of the modulo operation is an equivalence class, and any member of the class may be chosen as representative.
The usual representative is the least positive residue, e.g. \(-16 \text{ mod } 5 = 19 \text{ mod } 5 = 4\).
However, programming languages and calculators have various ways of storing and
representing numbers, so their convention may differ. Some languages like C++
have the result of a modulo operation share the same sign as the dividend, e.g.
-16 % 5 == -1 and 19 % 5 == 4.
Failing to understand this difference may lead to bugs, e.g. a program such as:
bool is_odd(int n) {
// If n is -ve, then n % 2 may return -1, reporting an incorrect result.
return n % 2 == 1;
}
References
- Cryptography | Computer science | Computing | Khan Academy. www.khanacademy.org . Accessed Jan 8, 2022.
- Modulo operation - Wikipedia. en.wikipedia.org . Accessed Jan 8, 2022.
Without visualizing a clock \(-17 \text{ mod } 7 = -3 \), but our mod operator is defined to give positive results. We therefore do \(7 - 3 = 4\).