Minimum Penalty for a Shop

Minimum Penalty for a Shop. leetcode.com . Accessed Jul 21, 2024.

Problem

You are given the customer visit log of a shop represented by a zero-indexed string customers consisting only of characters N and Y. If the \(i^{th}\) character is Y, it means that customers come at the \(i^{th}\) hour, whereas N indicates that no customers come at the \(i^{th}\) hour.

If the shop closes at the \(j^{th}\) hour (\(0 \le j \le n\)), the penalty is calculated as follows:

For every hour when the shop is open and no customers come, the penalty increases by \(1\).
For every hour when the shop is closed and customers come, the penalty increases by \(1\).

Return the earliest hour at which the shop must be closed to incur a minimum penalty. Note that if the shop closes at the \(j^{th}\) hour, it means the shop is closed at the hour \(j\).

Solution

Consider the string YYNY. There are two parts to the penalty at each hour:

Hour	Pre-Close Penalty	Post-Close Penalty	Penalty
0	0	3 `YYNY`	3
1	0 `Y`	2 `YNY`	2
2	0 `YY`	1 `NY`	1
3	1 `YYN`	1 `Y`	2
4	1 `YYNY`	0	1

The pre-close and post-close penalties are both monotonic. At each step, there is a penalty of \(1\) that either goes to either increasing the pre-close penalty or decreasing the post-close penalty.

Implementation

def best_closing_time(customers: str) -> int:
    # Set the initial values.
    suffix_penalty = sum(1 if c == 'Y' else 0 for c in customers)
    prefix_penalty = 0
    best_hour = 0
    min_penalty = suffix_penalty + prefix_penalty

    # Review the rest of the string and update the best value found.
    for hour in range(1, len(customers) + 1):
        if customers[hour-1] == 'Y':
            suffix_penalty -= 1
        else:
            prefix_penalty += 1

        penalty = prefix_penalty + suffix_penalty
        if penalty < min_penalty:
            best_hour = hour
            min_penalty = penalty

    return best_hour

Runtime \(\mathcal{O}(N)\). Space usage: \(\mathcal{O}(1)\).

I’ve seen this pattern before in Minimizing Bottom-Right Paths in a 2xN Grid , where we have a initial value that we update on seeing the next item in the collection.

Learnings

tags this problem with “Prefix Sum”, a class of problems that feature the pattern \(y_i = y_{i-1} + x_i\). #prefix-sum

We do not need to separately maintain prefix_penalty and suffix_penalty.

Implementation with single penalty value

def best_closing_time(customers: str) -> int:
    # Set the initial values. Assume that we are closed at hour 0.
    penalty = sum(1 if c == 'Y' else 0 for c in customers)
    earliest_closing_hour = 0
    min_penalty = penalty

    # Try closing the shop at hours 1, ..., n-1
    for latest_open_hour, c in enumerate(customers):
        # If there is a customer at this hour, moving it to open hours
        # decreases the penalty by one. If there's no customer, then we
        # incur a penalty by having the shop open.
        penalty += -1 if c == 'Y' else 1

        if penalty < min_penalty:
            earliest_closing_hour = latest_open_hour + 1
            penalty = min_penalty

    return earliest_closing_hour

From a pure refactor perspective, could I have been able to infer this?

prefix_penalty = 0
suffix_penalty = sum(1 if c == 'Y' else 0 for c in customers)
min_penalty = prefix_penalty + suffix_penalty

for hour in range(1, len(customers) + 1):
  if customers[hour-1] == 'Y': suffix_penalty -= 1
  else: prefix_penalty += 1
  penalty = prefix_penalty + suffix_penalty

min_penalty is trivially suffix_penalty because prefix_penalty is \(0\).

In the Y case, penalty = prefix_penalty + suffix_penalty - 1, while in the N case, penalty = prefix_penalty + 1 + suffix_penalty. Therefore, prefix_penalty + suffix_penalty can be collapsed into one value.

In the rewrite, using for latest_open_hour, c in enumerate(customer) instead of for hour in range(1, len(customers) + 1) clarified my thinking a lot. Another point for selecting good variable names and using idiomatic constructs.

The initial pass over customers gets us the starting penalty. However, the question asks for the earliest hour with the lowest penalty, and so it’s the penalty of the hours relative to each other that matters, not the specific penalty value.

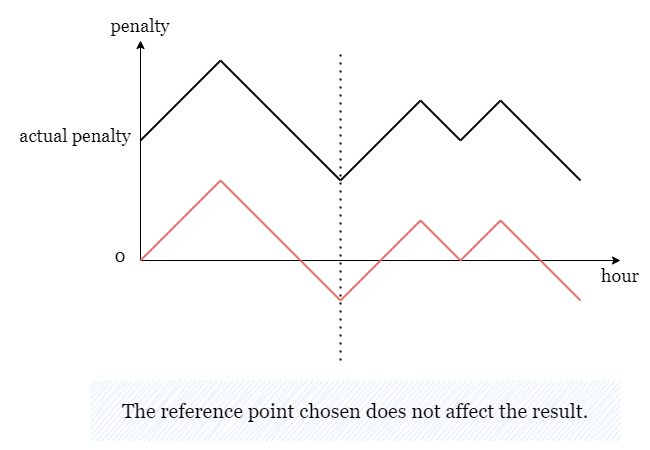
The reference shifts the graph up or down. However, the shape of the graph does not change. Source: leetCode2483Editorial

Implementation in a single pass

def best_closing_time(customers: str) -> int:
    # Assume that we are closed at hour 0. Set zero as the reference
    # point.
    penalty = 0
    earliest_closing_hour = 0
    min_penalty = penalty

    for latest_open_hour, c in enumerate(customers):
        # If there is a customer at this hour, moving it to open hours
        # decreases the penalty by one. If there's no customer, then we
        # incur a penalty by having the shop open.
        penalty += -1 if c == 'Y' else 1

        if penalty < min_penalty:
            earliest_closing_hour = latest_open_hour + 1
            min_penalty = penalty

    return earliest_closing_hour

References

Prefix sum - Wikipedia. en.wikipedia.org . Accessed Jul 21, 2024.
Minimum Penalty for a Shop > Editorial. leetcode.com . Accessed Jul 21, 2024.