Problem
A queen is standing on an \(n \times n\) chess board. The chess board’s rows are numbered from \(1\) to \(n\), going from bottom to top. Its columns are numbered from \(1\) to \(n\), going from left to right. Each square is referenced by a tuple \((r, c)\), describing the row, \(r\), and column, \(c\), where the square is located.
The queen is standing at position \((r_q, c_q)\). In a single move, she can attack any square in any of the eight directions (left, right, up, down, and the four diagonals). However, there are obstacles on the chessboard, each preventing the queen from attacking any square beyond it on that path.
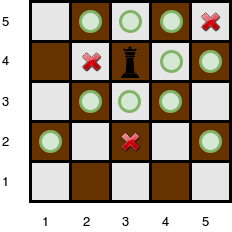
The queen at \((4, 3)\) on a \(5 \times 5\) chess board obstacles at \((2, 3)\), \((4, 2)\), and \((5, 5)\). The queen can attack \(10\) positions.
Given the queen’s position and the locations of all the \(k\) obstacles, find the number of squares that the queen can attack from her position at \((r_q, c_q\)).
Constraints:
- \(0 < n \le 10^5\)
- \(0 \le k \le 10^5\)
- A single cell may contain more than one obstacle.
- There will never be an obstacle at the position where the queen is located.
Solution
Starting from \((r_q, c_q\)), expand in each of the 8 directions until we run into an obstacle. In each loop, we choose the smallest update in that direction. This approach would traverse the list \(8\) times. Running time is \(\mathcal{O}(k)\).
We can also approach the problem from the outside shrinking in. Start by assuming that there are no obstacles, and then update the bounds in a single pass through the \(k\) obstacles. Running time is \(\mathcal{O}(k)\). I prefer this over the former as the former might have less cache locality when looping back from the beginning.
We can’t do better than \(\mathcal{O}(k)\) because we do need to see each obstacle at least once.
Implementation
"""
https://www.hackerrank.com/challenges/queens-attack-2/problem
"""
from typing import Tuple, List
def queens_attack(n: int, _: int, r_q: int, c_q: int, obstacles: List[Tuple[int, int]]):
"""
Given:
`n`: an integer, the number of rows and columns in the board
`k`: an integer, the number of obstacles on the board
`r_q`: integer, the row number of the queen's position
`c_q`: integer, the column number of the queen's position
`obstacles`: a 2D array of integers where each element is has the row and
column of an obstacle
The coordinates are one-based, not zero-based. (1, 1) is the south-west
corner of the board.
Return the number of squares that the queen can attack.
"""
south = r_q - 1
north = n - south - 1
west = c_q - 1
east = n - west - 1
north_east = min(north, east)
south_east = min(south, east)
south_west = min(south, west)
north_west = min(north, west)
def is_diagonal_to_queen(r, c):
"""Return True if (r, c) is on a diagonal to the queen."""
return abs(r - r_q) == abs(c - c_q)
for r, c in obstacles:
assert not (
r == r_q and c == c_q
), f"Obstacle ({r}, {c}) found on queen's position ({r_q}, {c_q})."
if c == c_q:
if r < r_q:
south = min(south, r_q - r - 1)
else:
north = min(north, r - r_q - 1)
elif r == r_q:
if c < c_q:
west = min(west, c_q - c - 1)
else:
east = min(east, c - c_q - 1)
elif is_diagonal_to_queen(r, c):
if r > r_q and c > c_q:
north_east = min(north_east, r - r_q - 1)
elif r > r_q and c < c_q:
north_west = min(north_west, r - r_q - 1)
elif r < r_q and c > c_q:
south_east = min(south_east, r_q - r - 1)
elif r < r_q and c < c_q:
south_west = min(south_west, r_q - r - 1)
limits = [
north,
north_east,
east,
south_east,
south,
south_west,
west,
north_west,
]
assert all(
limit >= 0 for limit in limits
), f"{limits} -ve after applying obstacle ({r}, {c}) to queen at ({r_q}, {c_q})"
return sum(
[north, north_east, east, south_east, south, south_west, west, north_west]
)
Tripping points:
- The indices are 1-based, and not 0-based. Had some off-by-one errors when computing the number of squares attackable in a given direction.
- Messing up the update logic. Adding the assertion at the end of the loop body that all 8 values are non-negative helped pinpoint where the error was.
Learnings from Editorial
features an algorithm that
expands out. When parsing the obstacle \((r, c)\), they flag it in a
map<pair<int, int>, int>, e.g., mp[{x, 1}] = 1. For each of the eight
starting positions, they get the number of free cells along that
direction:
bool in_range(int x, int y) {
return x <= n && x > 0 && y <= n && y > 0;
}
int num_free_cells(int x, int y, int dx, int dy) {
int ans = 0;
while(in_range(x, y) && !mp[{x, y}]) {
x += dx;
y += dy;
ans++;
}
return ans;
}
The std::map is not strictly necessary as we only need a presence
check. std::set would have sufficed. num_free_cells’s runtime is
\(\mathcal{O}(n)\). This approach uses \(\mathcal{O}(k)\) space. Why
does consider this an
\(\mathcal{O}(n)\) algorithm? They still need to parse the \(k\)
obstacles, and so shouldn’t it be \(\mathcal{O}(k + n)\)?
References
- Queen's Attack II > Editorial. www.hackerrank.com . Accessed Jul 20, 2024.