Minimizing Bottom-Right Paths in a 2xN Grid

Grid Game - LeetCode. leetcode.com . Accessed Jul 20, 2024.

Problem

You are given a 0-indexed 2D array grid of size \(2 \times n\), where grid[r][c] represents the number of points at position \((r, c)\) on the matrix. Two robots are playing a game on this matrix.

Both robots initially start at \((0, 0)\) and want to reach \((1, n-1)\). Each robot may only move to the right or down.

At the start of the game, the first robot moves from \((0, 0)\) to \((1, n-1)\), collecting all the points from the cells on its path. For all cells \((r, c)\) traversed on the path grid[r][c] is set to \(0\). Then, the second robot moves from \((0, 0)\) to \((1, n-1)\), collecting the points on its path. Note that their paths may intersect with one another.

The first robot wants to minimize the number of points collected by the second robot. In contrast, the second robot wants to maximize the number of points it collects. If both robots play optimally, return the number of points collected by the second robot.

The input grid is \([[2, 5, 4], [1, 5, 1]]\). The first robot takes the optimal path in red resulting in \([[0, 0, 4], [1, 0, 0]]\). The second robot will take the optimal path collecting \(0 + 0 + 4 + 0 = 4\).

Constraints:

grid.length == 2
n == grid[r].length
\(1 \le n \le 5 \cdot 10^4\)
\(1 \le \texttt{grid[r][c]} \le 10^5\)

Buggy Implementation

Given a grid, computing the maximum score that we can collect is a dynamic programming problem. At each grid[r][c], we pick the higher score from either the path that led us to grid[r-1][c] or grid[r][c-1]. This technique solves the second part of the problem.

Is minimizing \(R_2\)’s score equivalent to maximizing \(R_1\)’s score? Suppose there are \(P\) paths to \((1, n-1)\), where some path \(p_{max}\) has the highest score. \(R_1\) needs to take away \(p_{max}\) but is that sufficient? Can \(R_1\) choose a path that makes \(p_{max}\) impossible for \(R_2\) without necessarily taking \(p_{max}\) itself? Maximizing \(R_1\)’s score is not the optimal strategy as shown by this failing code:

Buggy Implementation

def grid_game(grid: List[List[int]]) -> int:
    def maximum_path(r, c) -> GridPath:
        # Base case: We need to pick up the points at (0, 0).
        if r == 0 and c == 0:
            return GridPath([(r, c)], grid[r][c])

        best_score = -inf
        best_path: List[Tuple[int, int]] = []

        # Choose the best option from the top and left neighbors.
        for (dr, dc) in [(0, -1), (-1, 0)]:
            new_r, new_c = r + dr, c + dc
            if new_r < 0 or new_c < 0:
                continue
            path, score = maximum_path(new_r, new_c)
            if score > best_score:
                best_score = score
                best_path = path

        return GridPath(best_path + [(r, c)], best_score + grid[r][c])

    # Let the first robot collect the max points.
    path_r1, _ = maximum_path(1, n - 1)
    for r, c in path_r1:
        grid[r][c] = 0

    # Then have the second robot try its best.
    _, score_r2 = maximum_path(1, n - 1)
    return score_r2

Learnings from Published Solution

Here’s a simpler counter-example for the hypothesis that maximizing \(R_1\)’s score minimizes \(R_2\)’s score:

10 50 50 30 --> R1 collects 150 --> 00 00 00 00 --> R2 collects 110
50 50 10 10                         50 50 10 00

If \(R_1\) can be less greedy, then it can force a lower score for \(R_2\):

10 50 50 30 --> R1 collects 120 --> 00 00 50 30 --> R2 collects 80
50 50 10 10                         50 00 00 00

\(R_1\) and \(R_2\) can move down only once. There are \(N\) possible paths.

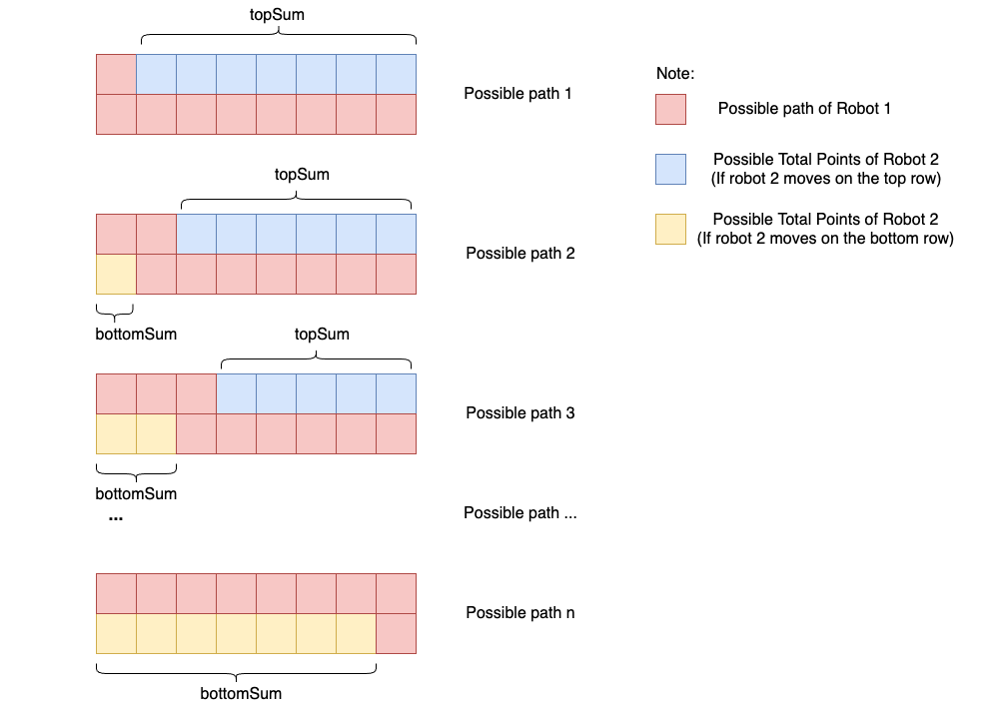
For each path traversed by \(R_1\), the max points that \(R_2\) can get are either the points left on the top row, or those left on the bottom row. Credits: hiepit2021

Implementation

"""
https://leetcode.com/problems/grid-game/description/
"""

from typing import List


def grid_game(grid: List[List[int]]) -> int:
    """
    Given a `2 x n` grid, find the maximum score obtainable by a robot `r_2`
    if there is a robot `r_1` that takes a first pass at the grid and zeroes
    out one path from (0, 0) to (1, n-1). Each robot starts from (0, 0) and can
    only move right/down.
    """
    assert len(grid) == 2, f"Expected 2 rows, found {len(grid)}"

    n = len(grid[0])
    assert all(len(row) == n for row in grid), f"All rows must have length {n}"

    # Set the initial candidates
    top_sum = sum(grid[0][1:])
    bottom_sum = 0
    best_r2_score = top_sum

    # Evaluate the rest of the N-1 paths and minimize `best_r2_score`.
    for drop_idx in range(1, n):
        top_sum -= grid[0][drop_idx]
        bottom_sum += grid[1][drop_idx - 1]
        best_r2_score = min(best_r2_score, max(top_sum, bottom_sum))

    return best_r2_score

References

[C++/Java/Python] Robot1 Minimize TopSum and BottomSum of Robot 2 - Picture Explained. leetcode.com . Sep 25, 2021. Accessed Jul 20, 2024.