Models state transitions through differential equations over continuous time \(t\). Commonly used to model the spread of diseases.
Possible states that proportions of the population could be in at time \(t\) are: susceptible \(S(t)\), infected \(I(t)\), and recovered \(R(t)\)
The SI Model
Assumes that one can only move from state \(S\) to state \(I\), with probability \(\beta\).
$$ S'(t) = - \beta S(t) I(t);\ \ \ \ I'(t) = \beta S(t) I(t) $$
But recall that \( S(t) + I(t) = 1 \). Therefore:
$$ I'(t) = \beta \left( 1 - I(t) \right) I(t) = \beta \left( I(t) - I^2(t) \right) $$
The solution is:
$$ I(t) = \frac{ I(0) e^{\beta t} }{ S(0) + I(0) e^{\beta t} },\ \ \ \ S(t) = \frac{ S(0) }{ S(0) + I(0) e^{\beta t} } $$
The SIS Model
Assumes two possible transitions: \(S \to I \) with probability \(\beta\), and \(I \to S\) with probability \(\gamma\).
$$ S'(t) = \gamma I(t) - \beta S(t) I(t);\ \ \ \ I'(t) = \beta S(t) I(t) - \gamma I(t) $$
The solution for \(I(t)\) is:
$$ I(t) = \left( 1 - \frac{\gamma}{\beta} \right) \left( \frac{ Ce^{(\beta - \gamma)t} }{ 1 + Ce^{(\beta - \gamma)t} } \right) $$
If \( \beta < \gamma \), \(I(t)\) decreases exponentially. If \( \beta > \gamma \), \(I(t)\) will increase, albeit asymptotically to \(1\).
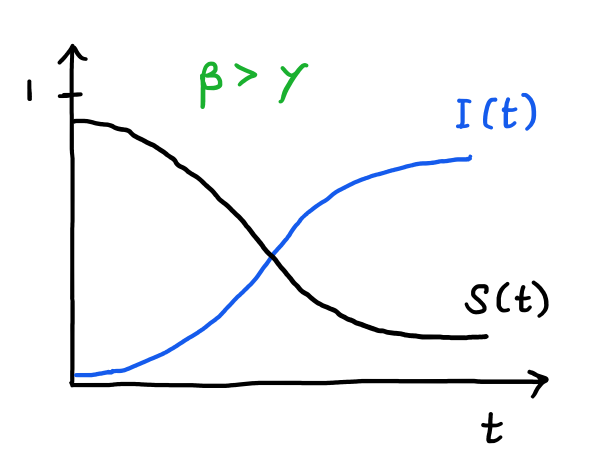
The SIR Model
Assumes two possible transitions: \(S \to I\) with probability \(\beta\), and \(I \to R\) with probability \(\gamma\).
$$ S'(t) = -\beta S(t) I(t);\ \ \ \ I'(t) = \beta S(t) I(t) - \gamma I(t);\ \ \ \ R'(t) = \gamma I(t) $$
Tip: \( \sigma = \frac{\beta}{\gamma} \) is the basic reproduction number.
If \( \sigma S(0) < 1 \), then \(I(\infty) = 0\), i.e. the initial \(S(0)\) isn’t large enough to create an epidemic.
If \( \sigma S(0) > 1 \), \(I(t)\) increases up to \( I(0) + S(0) - \frac{1}{\sigma} - \frac{ log(\sigma(S(0))) }{\sigma} \), and then decreases to \(0\) as \(t \to \infty \).
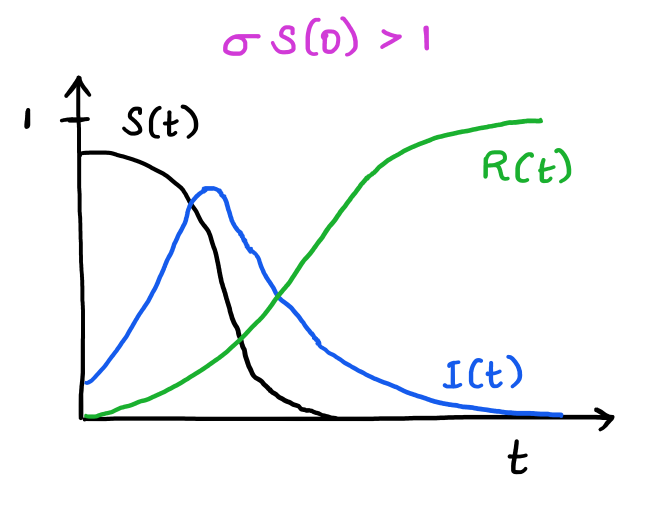
\( S(t) \) is always a decreasing function. The limit as \(t \to \infty \) is the unique root in the range \((0, 1/\sigma)\):
$$ I(0) + S(0) - S(\infty) + \frac{1}{\sigma} log\left( \frac{S(\infty)}{S(0)} \right) = 0 $$
References
- The Mathematics of Gossip. Jessica Deters; Izabel P. Aguiar; Jacquie Feuerborn. Community of Ordinary Differential Equations Educators, Vol. 12, Article 7. scholarship.claremont.edu . Feb 13, 2019.
The SIR model has also been used to model gossip.