A shortest path from vertex \(s\) to vertex \(t\) in an edge-weighted digraph is a directed path from \(s\) to \(t\) with the property that no other path has a lower weight.
A shortest-paths tree for a source \(s\) is a subgraph containing \(s\) and all the vertices reachable from \(s\) that forms a directed tree rooted at \(s\) such that every tree path is a shortest path in the digraph.
Properties of Shortest Paths
A shortest path must respect the direction of its edges.
The weights are not necessarily distances (albeit useful because of geometric intuition). Weights can be time, cost, etc.
Not all vertices need to be reachable. If \(t\) is not reachable from \(s\), there is no path at all, and therefore there is no shortest path.
Negative weights introduce complications.
Shortest paths are normally simple. The algorithms ignore zero-weight edges that form cycles, so the shortest paths found have no cycles.
There may be multiple paths of the lowest weight. The algorithms are content to find any one of them.
Parallel edges and self-loops may be present. However, only the lowest-weight among a set of parallel edges play a role in the algorithms. No shortest path contains a self-loop (except a zero-weight one, which the algorithms ignore).
Edge-Weighted Digraph Data Types
readonly record struct DirectedEdge(int From, int To, double Weight);
interface IEdgeWeightedDigraph
{
int V(); // Number of vertices
int E(); // Number of edges
void addEdge(DirectedEdge e);
IEnumerable<DirectedEdge> adj(int v); // Edges pointing from v
IEnumerable<DirectedEdge> edges(); // All edges in this digraph
}
interface IShortestPaths
{
double distTo(int v); // Infinity if no path
bool hasPathTo(int v);
IEnumerable<DirectedEdge>? pathTo(int v); // Null if no path, [] if v == s
}
All of the work in IShortestPaths is done in the constructor. How much of the
previous computation is reusable if we want to add a DirectedEdge and see the
effect on the shortest path? When evaluating Chicago’s metro for an undergrad
project, we pretty much recreated the graph whenever we wanted to test
addition/removal of a node (station) or edge (line connection) .
’s IShortestPaths uses a vertex-indexed array
edgeTo, where edgeTo[v] is the last DirectedEdge on a shortest path from
\(s\) to \(v\). It also uses a vertex-indexed distTo, where distTo[v] is
the length of the shortest known path from \(s\) to \(v\). By convention,
edgeTo[s] is null, distTo[s] is 0, and the distance to vertices
unreachable from \(s\) is \(\infty\).
Core Operation: Relaxation
Relaxation is at the core of IShortestPaths implementations in . To relax an edge \(v \to w\):
private void relax(DirectedEdge e)
{
var (v, w) = (e.From, e.To);
if (distTo[w] > distTo[v] + e.Weight)
{
distTo[w] = distTo[v] + e.Weight;
edgeTo[w] = e;
}
}
An ineligible edge \(v \to w\) is one where
distTo[v] + e.Weight >= distTo[w]; such edges are ignored. An edge \(v \to
w\) can be successfully relaxed if relax() would change the values of
distTo[w] and edgeTo[w].
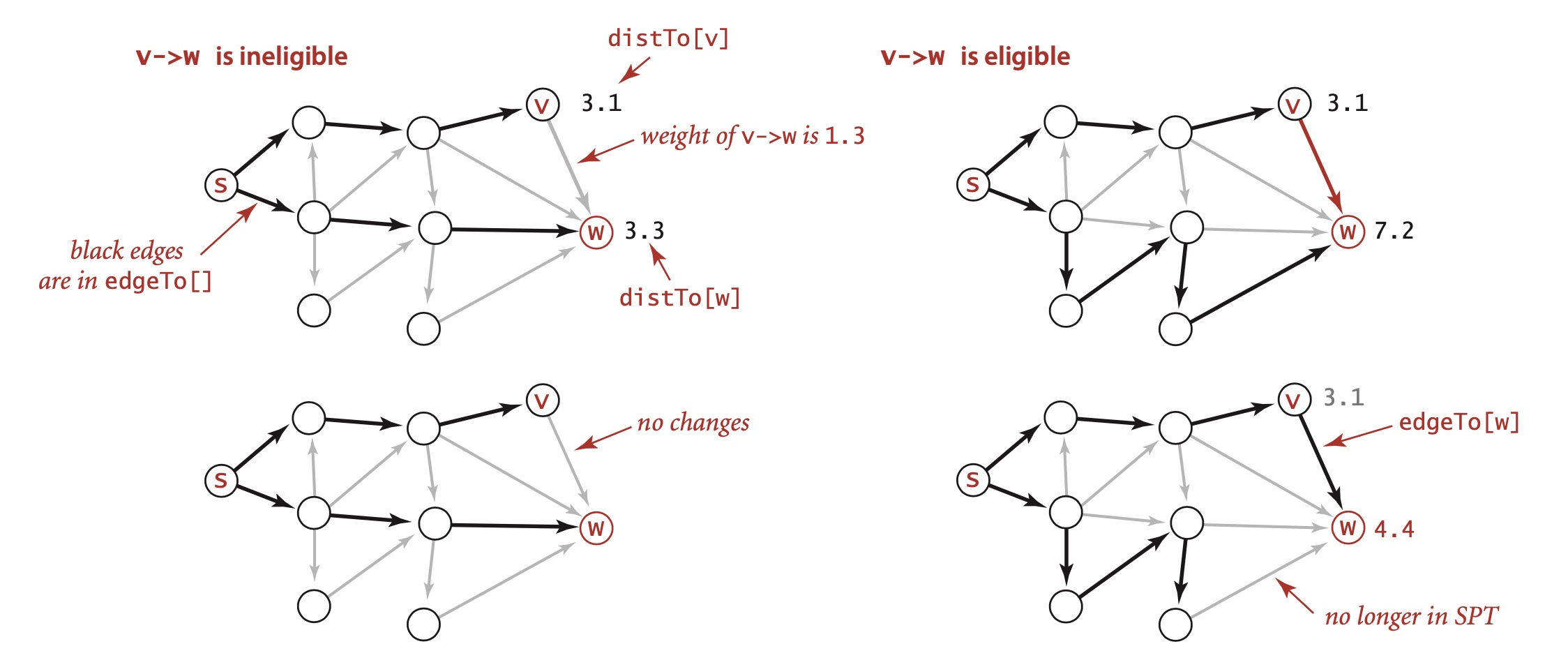
Two cases for edge relaxation; credits Sedgewick2011. Notice the effect of an eligible edge: some other edge gets booted out of the shortest paths tree.
To relax a vertex \(v\), we relax all the edges pointing from \(v\). Any
edge from a vertex whose distTo[v] is finite to a vertex whose distTo[w] is
\(\infty\) is eligible. Some edge leaving \(s\) is the first to be added to
edgeTo[]. IShortestPaths implementations choose vertices judiciously so that
each vertex relaxation finds a shorter path than the best known so far.
Theoretical Basis for Shortest-Paths Algorithms
Edge-relaxation is an easy-to-implement operation. The following proposition
shows an equivalence between the global condition that the distances in distTo
are shortest-paths distances, and the local condition we use to relax an edge.
I’ve seen this technique before in AoC 2024 Day 12: Garden Groups . The task was to count the number of sides in polygon composed of square tiles. Counting the number of corners a tile contributed is a local operation. A useful insight is that the number of corners in a polygon also equals the number of sides. Counting corners was far simpler than directly counting the sides.
Proposition: Shortest-Paths Optimality Conditions
Proposition: The values in distTo[] are the lengths of the shortest paths
if and only if distTo[w] <= distTo[v] + e.Weight for each edge \(v \to
w\).
If distTo[w] > distTo[v] + e.Weight for some e, then e would give a path
\(s \to … \to v \to w\) of length less than distTo[w], a contradiction.
The optimality conditions are thus necessary.
Suppose \(v_0 \to v_1 \to v_2 \to … \to v_k\) is a shortest path from
\(s\) to \(w\) of weight \(OPT_{sw}\). Denote \(v_{i-1} \to v_{i}\) as
\(e_i\). By the optimality conditions, and the fact that distTo[s] = 0:
$$ \text{distTo}[w] \le e_{1}.\text{weight} + … + e_{k}.\text{weight} = \text{OPT}_{sw} $$
Because distTo[w] is the length of some path from \(s\) to \(w\), it
can’t be smaller than the length of a shortest path. Therefore,
\(\text{OPT}_{sw} \le \text{distTo}[w] \le \text{OPT}_{sw}\), implying
equality. The optimal conditions are sufficient.
This proposition helps in certification. However, an algorithm computes
distTo, we can check whether it contains shortest-path lengths in a single
pass through the edges of the graph, checking whether the optimality conditions
are satisfied.
Proposition: Generic Shortest-Paths Algorithm
- Initialize
distTo[s] = 0and \(\infty\) for all otherdistTo[]. - Relax any edge in \(G\), continuing until no edge is eligible.
The generic algorithm works because:
- For any reachable vertex \(w\), some edge on the shortest path to \(w\) is eligible as long as \(\text{distTo}[w] = \infty\), and so the algorithm continues.
- For any reachable vertex \(v\), throughout the algorithm,
distTo[v]is the length of some (simple) path from \(s\) to \(v\) and is strictly monotonically decreasing. It can decrease at most a finite number of times. - When no edge is eligible, Proposition: Shortest-Paths Optimality Conditions applies.
The generic algorithm does not specify the order in which the edges are to be relaxed. To prove that any algorithm computes shortest paths, then all we need to do is prove that it relaxes edges until no edge is eligible.
Dijkstra’s Algorithm
- Initialize
distTo[s] = 0and \(\infty\) for all otherdistTo[]. - Relax and add to the tree a non-tree vertex with the lowest
distTo[]value, continuing until all vertices are on the tree, or no non-tree vertex has a finitedistTo[]value.
Dijkstra’s algorithm starts out with a priority queue with s in it. While pq
is not empty, relax pq.delMin():
private void relax(EdgeWeightedDigraph G, int v)
{
for (DirectedEdge e in G.adj(v))
{
int w = e.To;
if (distTo[w] > distTo[v] + e.Weight)
{
distTo[w] = distTo[v] + e.Weight;
edgeTo[w] = e;
if (pq.contains(w)) pq.change(w, distTo[w]);
else pq.insert(w, distTo[w]);
}
}
}
Dijkstra’s algorithm solves the single-source shortest-paths problem in edge-weighted digraphs with non-negative weights because:
- If \(v\) is reachable from \(s\), every \(v \to w\) is relaxed exactly
once. When \(v\) is relaxed,
distTo[w] <= distTo[v] + e.Weight. This inequality holds throughout because:distTo[v]never changes because edge weights are non-negative and we choose the lowestdistTo[]value at each step. No subsequent relaxation can improve ondistTo[v].distTo[w]can only decrease because any relaxation can only decrease it.
- After all vertices reachable from \(s\) have been added to the tree, Proposition: Shortest-Paths Optimality Conditions applies.
Alternatively, view Dijkstra’s algorithm as growing the tree by adding next the non-tree vertex that is closest to \(s\):
distTo[]entries for the tree vertices are shortest-paths distances.- For each \(w\) on the
pq,distTo[w]is the weight of the shortest path from \(s\) to \(w\) that uses only intermediate vertices in the tree and ends in the crossing edgeedgeTo[w]. - The
distTo[]for the vertex with the smallest priority is a shortest-path weight, not smaller than the shortest-path to any vertex already relaxed, and not larger than the shortest-path weight to any vertex not yet relaxed. That vertex is the next to be relaxed.
Dijkstra’s algorithm can also be modified to solve other versions of the problem:
- Single-source shortest paths in undirected graphs. Given an edge-weighted
undirected graph and a source vertex \(s\), support queries for the shortest
path to a given target vertex \(v\).
- Build an edge-weighted digraph with the same vertices and two directed edges (one in each direction) for each edge in the undirected graph. Solve using Dijkstra’s algorithm.
- Source-sink shortest paths. Given an edge-weighted digraph, a source
vertex \(s\), and a target vertex \(t\), find the shortest path from
\(s\) to \(t\).
- Use Dijkstra’s algorithm, but terminate as soon as \(t\) comes off the priority queue.
- All-pairs shortest paths. Given an edge-weighted digraph, support queries
for the shortest path from a source vertex \(s\) to a target vertex
\(t\).
- Solve Dijkstra \(V\) times, once for each \(v\) as the source, and cache those results.
References
- Algorithms, 4th Ed. Chapter 4: Graphs > 4.4: Shortest Paths. Robert Sedgewick; Kevin Wayne. algs4.cs.princeton.edu . ISBN: 978-0321573513 .
- transport_network_models/modifying_edges.py at master · dchege711/transport_network_models. github.com . Accessed Dec 14, 2025.
Rewritten from Java versions in to C# for brevity.